梯形中位线定理证明方法（12种方法证明梯形中位线定理）

广义对称思想有机会相等，利益均沾的内涵，是一种美妙的数学思想，它体现了运动的观点，是换个角度看问题的典范，同时又体现了数学的灵活性，它是数学一题多解，多解归一最强大的思维武器。

下面用12种方法对初高中衔接内容梯形的中位线定理进行证明，来体会广义对称的美妙与强大。

问题：如图，梯形ABCD中，AD∥BC,E、F分别是AB,CD的中点，如果EF=3，高为3，则梯形的面积是多少？

这道题对于没有学过梯形中位线定理的同学来说还是需要很强的转化分析能力的，但是如果用梯形中位线定理直接得到梯形的面积是3×3=9.

那么什么是梯形中位线定理如何证明？

梯形的中位线定理：梯形的中位线平行于上下底，并且等于上下底和的一半

如图，梯形ABCD中，AD∥BC,E、F分别是AB,CD的中点，求证:(1)EF∥AD∥BC(2)EF=½（AD+BC）

证明：方法一

方法1：

平行+中点延长得全等+三角形中位线

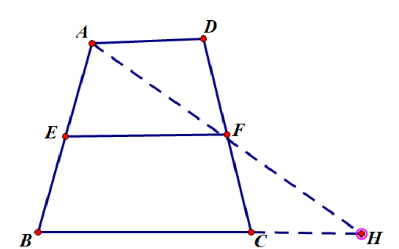
证明：如图连接AF并延长，与BC的延长线交于H.

∵AD∥BC

∴∠DAF=∠H

∵F是DC中点

∴DF=FC

又∵∠DFA=∠CFH

∴△DFA≌△CFH

∴AD=CH

∵,E、F分别是AB,CD的中点

∴EF是△ABH的中位线

∴EF=½BH=½（AD+BC）

∴EF∥BC∥AD

根据广义对称思想，A、B、C、D地位是平等的，因此也有过B、C、D构造平行+中点延长得全等的8字模型同样类似的结论。

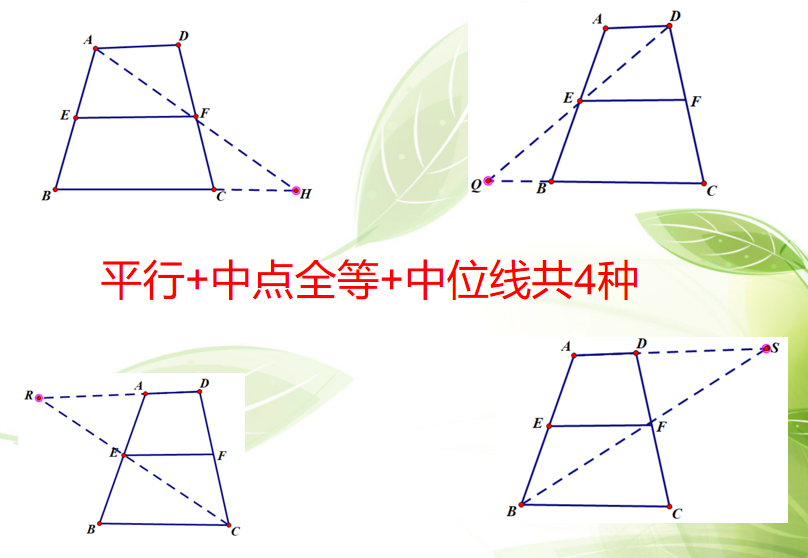
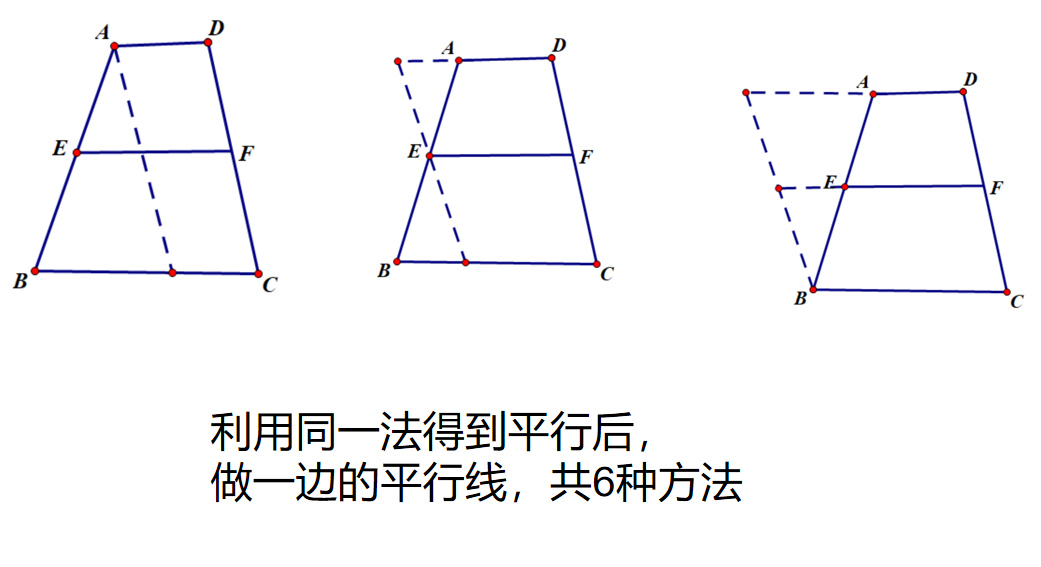
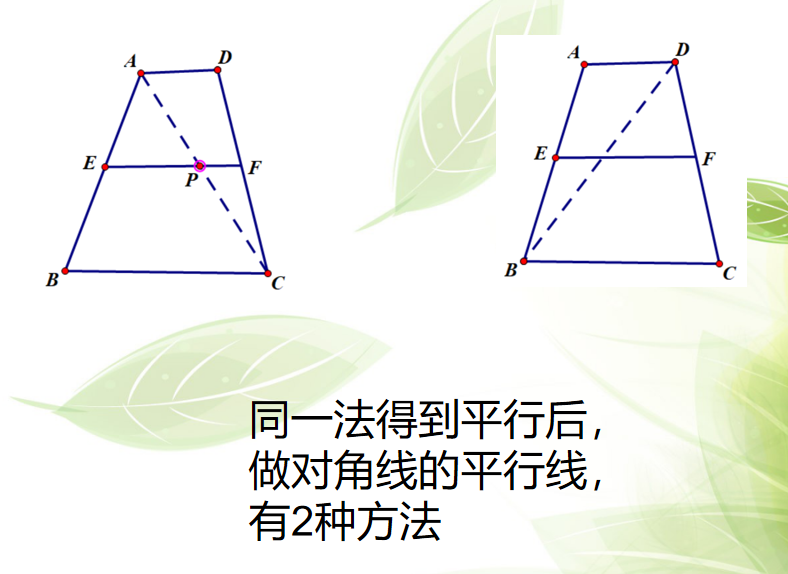
以上12种方法从平行线产生的角度看可以分为两大类，利用广义对称，可以知道每个基本元素点，都是具有相同的地位，可以随意轻松地完成，而且帮助我们理解本质。可见广义对称思想的强大之处，实际上初中它是一中特别重要的思维方式，在数学和生活中广泛应用，例如完全平方公式，三角形内角和证明，四边形内角和证明等。