1. 定向移动的平均速率

下面以铜导线为例，估算一下通电后内部自由电子定向移动的平均速率。

取铜的密度8.9×10^3kg/m3，铜的摩尔质量为6.35×10^-2kg/mol，则每立方米铜的物质的量为：

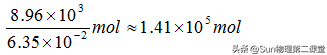
阿伏伽德罗常数NA=6.02×10^23/mol，每个铜原子提供2个自由电子，所以每立方米铜中含有的自由电子数（n）为：

电子的带电量（e）为1.60×10^-19C，一般铜导线的安全载流量（I/S）为5~8A/mm2，这里取5A/mm2。根据电流的微观表达式可知，电子定向移动的平均速率为：

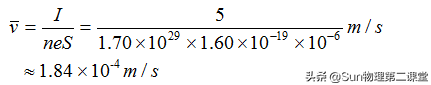
结果的数量级与教材是一致的！按这个定向移动的平均速率计算，一个电子通过一条长1m的铜导线大约需要的时间为：

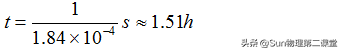
这个结果似乎与我们闭合电灯开关时的感觉不符。实际上，闭合开关的瞬间，导线中的各个位置以光速（c=3.0×10^8m/s）迅速建立了电场，内部的自由电子在静电力的作用下几乎同时开始做定向移动，所以整个电路也就几乎同时形成了电流。

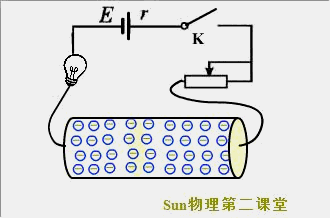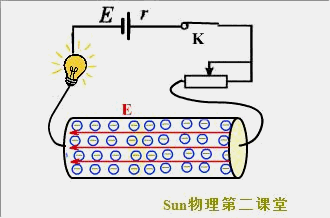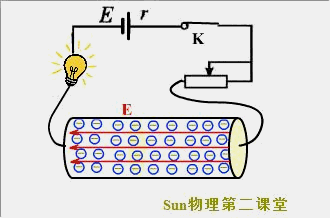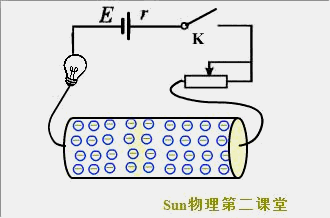
2.热运动的平均速率

通常情况下，金属导体中大量的自由电子都在做无规则的热运动，它们朝任何方向运动的几率都是相同的，所以对导体内的任何一个截面来说，任何一段时间内从截面两侧穿过截面的自由电子数都相等，因此从宏观上看，自由电子的热运动不能形成电流。

金属导体内自由电子的热运动与气体分子的热运动类似，其运动的剧烈程度都与温度有关。气体分子做无规则热运动时，速率有大有小，但大量分子的速率却按一定的规律分布，即呈现 呈“ 中 间 多、 两 头少 ” 的特点——麦克斯韦速率分布律。

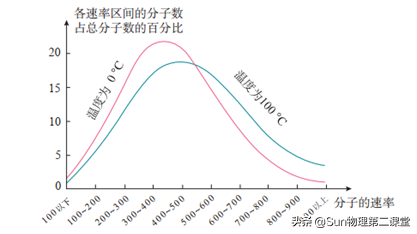
氧气分子的速率分布图像

一般将大量分子速率的算术平均值称为分子热运动的平均速率，且有：

其中k=1.38×10^-23J/K，为玻尔兹曼常数，T为热力学温度，它与摄氏温度t之间的关系为：T=273+t，m为分子的质量。利用这个规律可以估算金属导体内自由电子热运动的平均速率。电子的质量（m）为9.1×10^-31千克，通常状况下取温度t=20℃，则T=293K，代入热运动的平均速率公式可得：

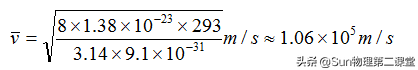
对比以上两个“平均速率”可以看出：金属导电时，内部自由电子定向移动的平均速率(约为 10^-4 m/s)要比自由电子热运动的平均速率(约为 10^5 m/s)小很多，它与电流的传导速率，即电场的传播速率（c=3.0×10^8m/s）也不是一回事！

足球在空中运动时，球内的分子在做无规则热运动的同时还共同参与足球的运动